Boundary Value Caching for Walk on Spheres

Bailey Miller* , Rohan Sawhney* , Keenan Crane† , Ioannis Gkioulekas†

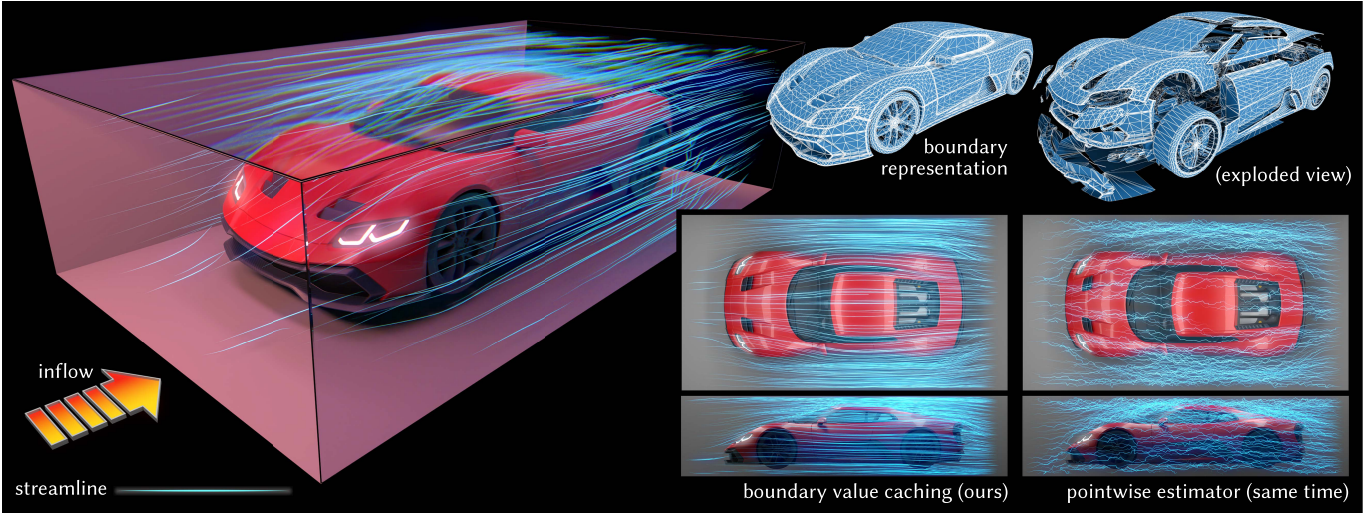
Our caching scheme dramatically reduces the total number of random walks needed to solve partial differential equations relative to classic pointwise Monte Carlo estimators. Here we show streamlines of a flow in a simulated wind tunnel, computed directly from a low-quality surface mesh originally intended for visualization rather than simulation.

Abstract

Grid-free Monte Carlo methods such as walk on spheres can be used to solve elliptic partial differential equations without mesh generation or global solves. However, such methods independently estimate the solution at every point, and hence do not take advantage of the high spatial regularity of solutions to elliptic problems. We propose a fast caching strategy which first estimates solution values and derivatives at randomly sampled points along the boundary of the domain (or a local region of interest). These cached values then provide cheap, output-sensitive evaluation of the solution (or its gradient) at interior points, via a boundary integral formulation. Unlike classic boundary integral methods, our caching scheme introduces zero statistical bias and does not require a dense global solve. Moreover we can handle imperfect geometry (e.g., with self-intersections) and detailed boundary/source terms without repairing or resampling the boundary representation. Overall, our scheme is similar in spirit to virtual point light methods from photorealistic rendering: it suppresses the typical salt-and-pepper noise characteristic of independent Monte Carlo estimates, while still retaining the many advantages of Monte Carlo solvers: progressive evaluation, trivial parallelization, geometric robustness, etc. We validate our approach using test problems from visual and geometric computing.

Resources

Publication

Paper

Publisher's Version

ArXiv Version

Code

Github project with full source code

Videos

Citation

        
    @article{
      Miller:BVC:2023,
      title={Boundary Value Caching for Walk on Spheres},
      volume={42},
      ISSN={1557-7368},
      url={http://dx.doi.org/10.1145/3592400},
      DOI={10.1145/3592400},
      number={4},
      journal={ACM Transactions on Graphics},
      publisher={Association for Computing Machinery (ACM)},
      author={Miller, Bailey and Sawhney, Rohan and Crane, Keenan and Gkioulekas, Ioannis},
      year={2023},
      month=jul, 
      pages={1-11}
    }

Acknowledgements

This work was generously supported by nTopology and Disney Research, NSF awards 1943123, 2212290 and 2008123, Alfred P. Sloan Research Fellowship FG202013153, a Packard Fellowship, NSF Graduate Research Fellowship DGE2140739, and an NVIDIA Graduate Fellowship.